Building a simple model
What will you learn?
- Functors and ports
- Writing algebraic and logical expressions
A solution for a spatial model involves recovering maps from a cartographic model - that is a cube of registered raster maps, in which each map depicts a particular geographic feature -, processing them in an ordered way, and then storing the intermediate results for subsequent processing (Fig. 1).
To improve performance, the Dinamica EGO processing system only accesses the disk once to read the input maps, if enough memory is available, and then to write the final outputs(Fig. 2).
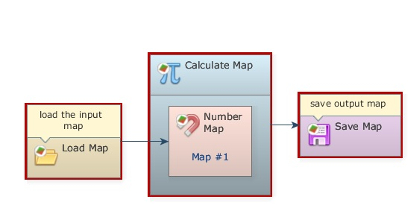
Thus a model in Dinamica EGO is represented by a sequence of functors, whose execution takes place from left to right. A simple model consists of a functor that loads the data, for example, a map, another functor that performs some calculation as well as one that writes the result into a file. Note that the functors are connected to each other through arrows. In order to do so, they must exchange compatible data via their outputs and inputs. Dinamica EGO input parameters and data, as well as the outputs from a functor, are called ports. Hence functors are connected via compatible input and output ports. Let’s start designing your first model in Dinamica EGO.
From the library window grab and place on the sketch the Load Map and Save Map functors, which are located in the Input/Output tab. Now grab the container Calculate Map from the Map Algebra tab. A container is a special type of functor that can envelope supplementary functors or even a sequence of functors. The containers differ from a functor by its action bar.
You should have something like this:
Now you need to connect the functors to establish a model. First, let’s understand what a Calculate Map does. This container is a calculator used for map algebra to combine and process maps, tables and constants. As a container, it does not function by itself. There is a need to add supplementary functors to it. In this case, each map processed by this container will be represented by the functor Number Map. Click in the hook tool  to create a hook functor with Number Map inside the container Calculate Map. The container will resize to accommodate the Number Map.
to create a hook functor with Number Map inside the container Calculate Map. The container will resize to accommodate the Number Map.
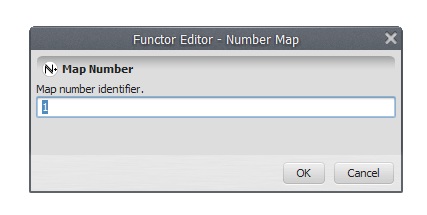
Click on the Number Map with the Functor Editor tool and enter “1” (do not write the quotation marks). This is a number identifier for a map and will be represented within the equation box as i1 (input 1). You can enter other maps by adding more Number Map functors, but each one must have a unique number identifier. Now you can connect the functor Load Map to the Number Map and the container Calculate Map to Save Map. Use the connect tool (the arrow icon) to establish the connections. Observe that the connection is set automatically because there is only one option for compatible ports in the respective functors and container.
Clicking on the arrow with the Edit Functor Ports tool allows us to visualize the links between a pair of functors.
Now that the functors are linked, you can rearrange the model by clicking on the execute layout. Note that the model will be organized
from left to right or left to bottom according to its execution sequence.
In the next step, open the Calculate Map container by grabbing the Edit Functor and clicking on it. Note that map #1 is represented by i1. The Calculate Map enables the formulation of various algebraic and logic equations containing maps, tables and constants.
Here you can find examples of operators that can be applied to process data within this container.
Besides writing the equation, there are two parameters that must be set. The Cell Type and the Null Value. You will always find these parameters in functors that produce maps as output. The default is “Signed 32 Bit Integer”, but you can use “IEEE 754 32 Bit Real” to represent fractional numbers.
Try to use always the most economical representation for data cell type to save memory. If you are not sure about the numeric range of the output, use real number representation.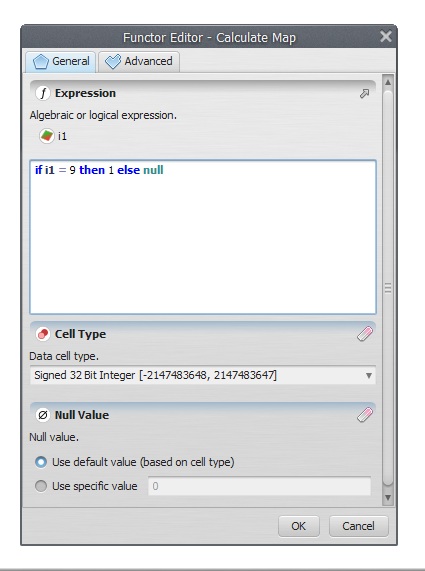
Now that you have learned the vast possibilities of this container, let’s write a simple equation:
if i1 = 9 then 1 else null
This means: Find the map class equal to 9, and set all others to null.
Set the Cell Type to “Unsigned 8 Bit Integer” and the Null Value to “Use default value”. Now you can close this container and open a map file to use as input for this model.
Open the Load Map functor and load the file amazon_states.tif from folder lesson1. You do not need to worry about the other options, they are not needed for now.
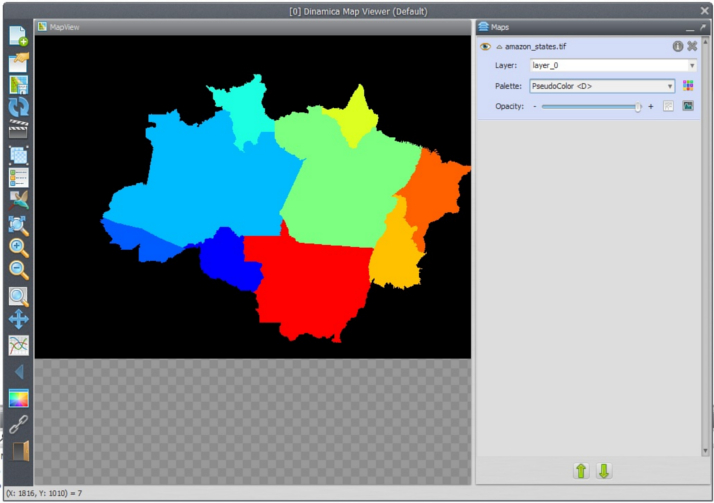
Open the Map Viewer to visualize this map. Press Histogram and then choose limits to actual and make sure that the current color palette is PseudoColor. Go to the Map viwer Tutorial if tou have any doubts. The map will look like this:
Now you need to save the result to a file. Open Save Map and write Mato_Grosso_state. 
In the Advanced tab there is an option to set the file name Suffix Digits. Although the default is 2, this parameter will be ignored since there is only one iteration.
Use Compression is only applicable for geotiff and img format.
The input map is a categorical map; its values do not represent quantities, but they are identifiers to map classes, thus representing categorical data as follows:
| Key | State |
|---|---|
| 1 | Rondonia |
| 2 | Acre |
| 3 | Amazonas |
| 4 | Roraima |
| 5 | Para |
| 6 | Amapa |
| 7 | Tocantins |
| 8 | Maranhao |
| 9 | Mato Grosso |
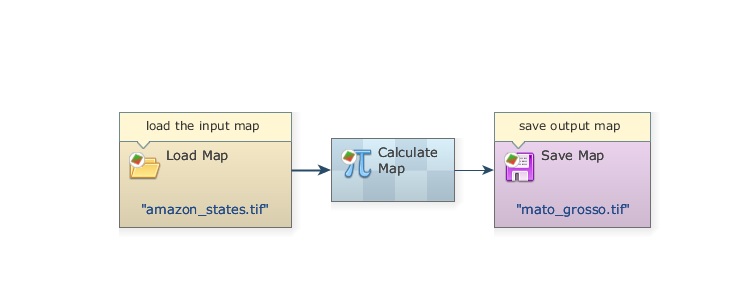
Minimize the Calculate Map container by clicking on its bar. The model should look like this:
Save the model as my_model in lesson1 folder, run the model by clicking on the run model script button on the top toolbar and open the result on the Map Viewer. The output map depicts only the Mato Grosso state.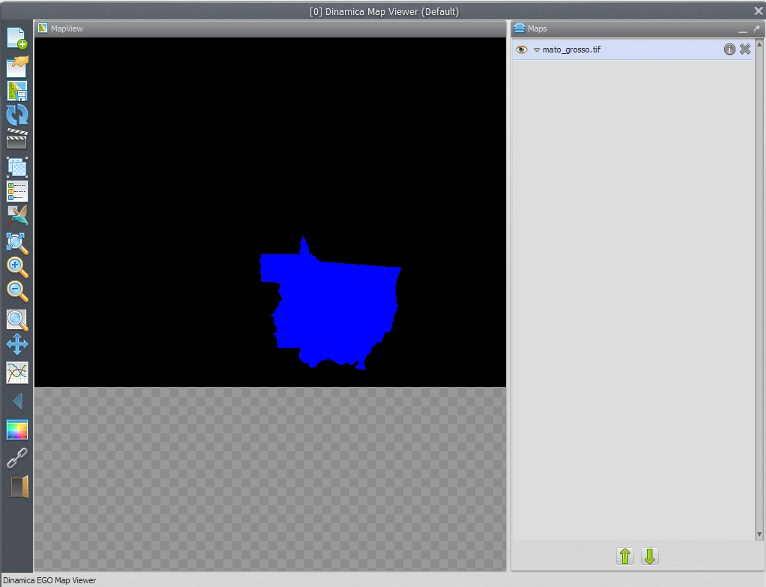
Congratulations, you have successfully completed this lesson! Now let’s move to the next ones!

